発表のポイント：

• 多くのLLMで採用されている位置符号化※1であるRotary Position Embedding(RoPE) ※2がウェーブレット変換の一種であることを解明し、ウェーブレット変換※3が位置符号化に有効である可能性を示しました。
• ウェーブレット変換を応用した独自の位置符号化を開発しました。この位置符号化はLLMの生成性能を改善するだけでなく、LLMの処理可能な長さを超えたテキストも生成可能とします。
• 従来行っていたLLMの最大系列長拡張のための追加の再学習が不必要となり、学習コスト低減という産業上重要な課題の解決に貢献できます。

　日本電信電話株式会社（本社：東京都千代田区、代表取締役社長：島田　明、以下「NTT」）は、ウェーブレット変換を応用したLLMの追加学習なしで決められた長さを超えるテキストを生成できる技術を世界で初めて開発しました。位置符号化はLLM内部における各単語の位置を表現する機構で、従来のLLMではRotary Position Embedding (RoPE) が採用されていました。本成果では、このRoPEがウェーブレット変換の一種であることを証明し、その他の位置符号化手法もウェーブレット変換のような特徴を持つことを示しました。また、ウェーブレット変換を応用した位置符号化を開発し、LLMの追加学習なしで決められた長さ以上のテキストを生成することが可能となります。これにより、従来行っていたLLMの最大系列長拡張が不必要となり、学習コストの低減を実現します。将来的には本技術のさらなる検証・改善を続け、NTTの大規模言語モデル「tsuzumi」への導入を目指していきます。
　本成果は、2025年4月24日に国際会議The Thirteenth International Conference on Learning Representations (ICLR 2025)にて発表されます。
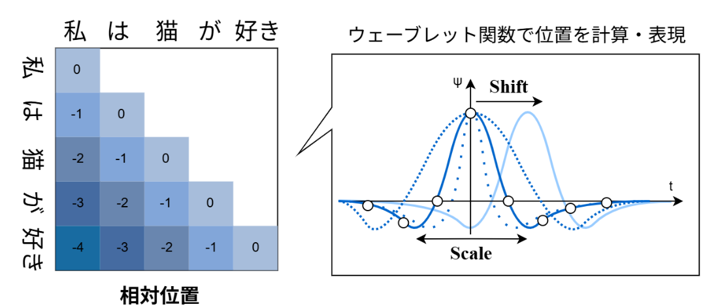
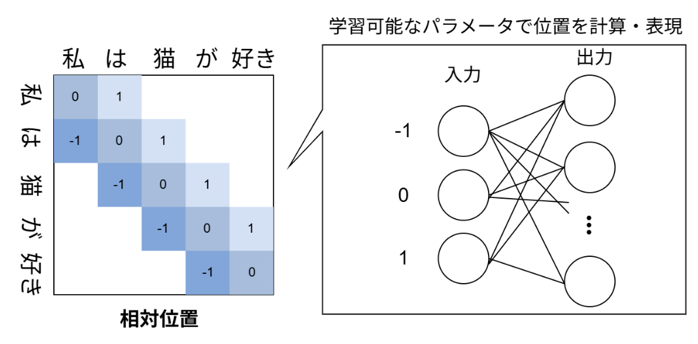
　　 図１: 本技術におけるLLM内部での位置の表現方法。各単語の「相対的な位置」をウェーブレット関数を使って計算する。このとき、スケールとシフトが異なるウェーブレット関数で計算する。

1．背景
　従来のＬＬＭは事前学習時の計算資源の制約から、テキストの最大系列長を事前に決める必要があります。このテキストの最大系列長より長いテキストを生成しようとすると、生成性能が大きく下がります。そのため、長いテキストで構成されたデータセットを使って追加で再学習を行うことが一般的ですが、計算資源を多く必要とする学習のコストが再度かかってしまうという課題があります。
　このような課題を解決するために、LLM内部で単語の位置を表現する「位置符号化」と呼ばれる仕組みを活用し、最大系列長を超える長文を生成する試みが多く行われています。
まず、位置符号化には実装上「絶対位置」と「相対位置」という二つの位置表現手法があります。「絶対位置」は文の先頭からの各単語の位置を表現しており、「相対位置」は文内の各単語同士の相対的な位置を表現しています。現在、多くのＬＬＭでは「絶対位置」を使い「二次元回転行列」を使って位置を表現する位置符号化Rotary Position Embedding (RoPE) が採用されています。RoPEでは、「クエリベクトル※4」を２次元ごとに分割し、二次元回転行列と分割したクエリベクトルとの内積を計算することで位置を表現します。「キーベクトル※4」に対しても同じ処理を行います。RoPEは計算が高速ではありますが、「絶対位置」を採用しているため、最大系列長より長い文を生成すると性能が下がってしまうという課題があります。
　一方で、「相対位置」では、各単語が他の単語とどの程度関連しているかを示す「注意スコア※5」に相対位置の値を足し合わせることで位置を表現するAttention with Linear Biases (ALiBi) ※6という手法が提案されており、最大系列長より長い文を生成しても性能が下がりません。しかし、ALiBiをＬＬＭに採用すると、モデルが遠い依存関係にある単語の情報を取得できない、さらに最大系列長より短い文の生成性能はRoPEより低いという課題があります。また、「相対位置」の別手法として、Relative Position Representation (RPE)※7という手法も提案されています。これは学習可能なパラメータで相対的な位置を表現し、クエリと内積を取ることで位置を表現しますが、ある一定の範囲、例えば前後１６トークンほどの決められた範囲でしか相対位置を表現しないことから、ALiBiほど外挿性能が高くないことがわかっています。


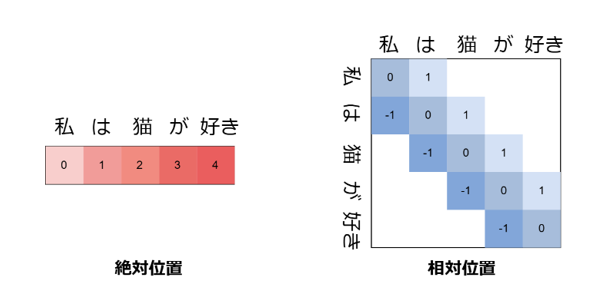
図２：LLM内部で単語の位置を表現する「位置符号化」における表現手法「絶対位置」と「相対位置」。絶対位置は、各単語の先頭からの位置を表現する。相対位置は、各単語から各単語への相対的な位置を表現する。


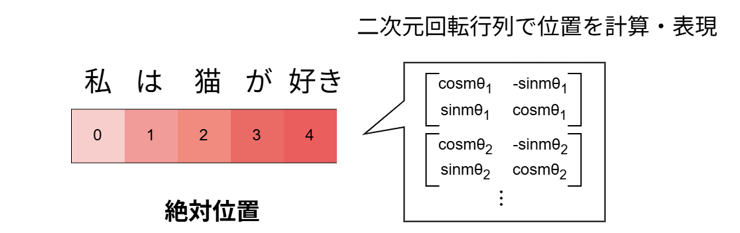
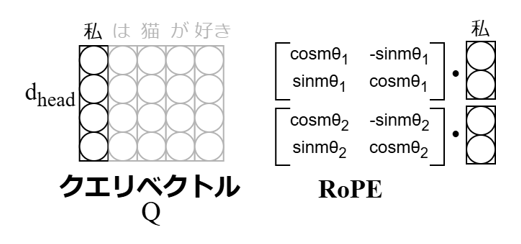
図３：「絶対位置」を使い回転行列を使って位置を表現する位置符号化Rotary Position Embedding (RoPE) の概要。絶対位置を回転行列によって計算する。


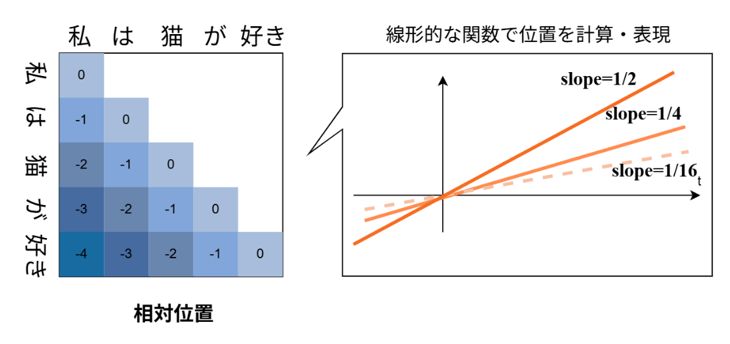
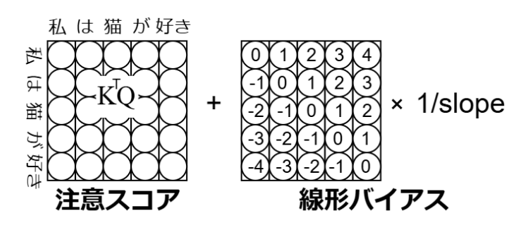
図４：相対位置を表現するAttention with Linear Biases (ALiBi) の概要図。すべての相対位置を線形的な関数を使って計算する。そのぞれ傾き(slope)が違う線形的な関数を複数使う。


図５：学習可能なパラメータで相対的な位置を表現するRelative Position Representation (RPE)の概要図。RPEでは相対位置は学習可能パラメータで表現される。また、RPEはある一定の範囲内の相対位置しか表現しない。本成果である「ウェーブレット位置符号化」はこの相対位置を学習可能パラメータではなく、ウェーブレット関数に基づいて計算し、すべての相対位置を計算します。

2．技術のポイント
　回転行列を使って位置を表現する位置符号化Rotary Position Embedding (RoPE) など従来の位置符号化は正弦波関数または余弦波関数によって位置を表現していたことから、サイン関数またはコサイン関数が位置表現に有効であると考えられてきました。しかし、今回、RoPEは信号処理における時間周波数解析の一種であるウェーブレット変換の一種と解釈できることを発見しました。さらに、相対位置の一種であるAttention with Linear Biases (ALiBi) は様々な分解能を組み合わせて位置を表現していることを発見しました。すなわち、さまざまな幅の視野で単語の位置を捉えています。この様々な分解能を組み合わせていることはウェーブレット変換の特徴も一致していることから、従来の位置符号化とウェーブレット変換に共通点があることを発見しました。
　これらの発見から、ウェーブレット変換が位置符号化に有効であると考え、ウェーブレット変換を応用した位置表現技術「ウェーブレット位置符号化」を開発しました。提案手法は相対位置をウェーブレット関数に基づいて計算を行い、各単語を表現するクエリベクトルとの内積を計算することでモデル内の単語の位置を表現します。すなわち、RPEの手法において学習可能パラメータで表現されていた位置をウェーブレット関数で計算します。このとき、分解能が異なる複数の波形を組み合わせることで、ALiBiのように様々な分解能で位置の表現が可能となるため、従来の位置符号化より生成性能が改善し、最大系列長を超える長文も性能を維持したまま生成可能です。さらに、RPEに基づいた本技術を用いることで、モデルは遠い箇所にある単語の情報も取得可能になります。


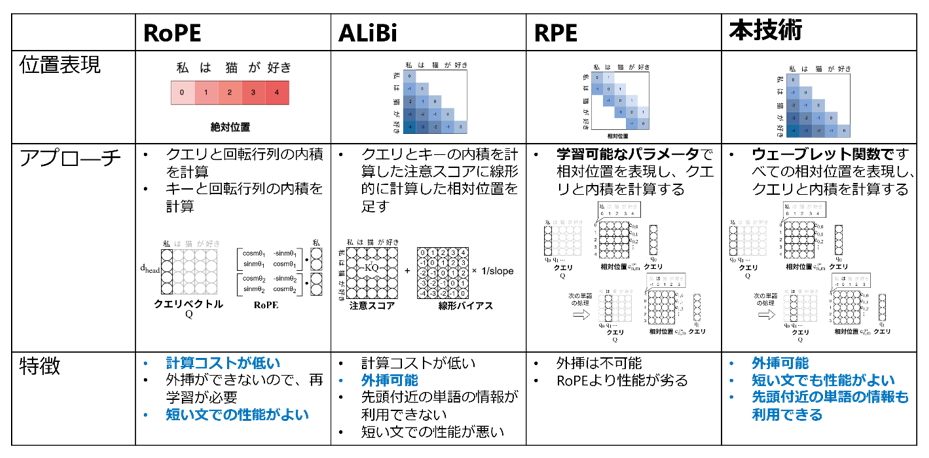
図６：各位置符号化を比較した表。

4．今後の展開
　今回開発した位置符号化を使うことでLLMの処理可能な長さを超えたテキストも生成可能となります。このことから、LLMの最大系列長拡張のための追加の再学習が不必要となり、学習コストの低減が見込めます。本技術が社会に浸透することによって、新規LLMの学習コストの低減と長文読解におけるLLMのさらなる性能改善が期待できます。長文読解の性能が向上することで、業務内容が記載されたマニュアルや、重要文書などの読解性能が向上し、業務の引き継ぎや社内教育が効率化されるとともに、法律文書や医療記録など専門性の高い文章の理解支援にも貢献することが期待されます。

【論文情報】
会議名： The Thirteenth International Conference on Learning Representations （ICLR 2025）
題 名： Wavelet-based Positional Representation for Long Context
著者名： Yui Oka, Taku Hasegawa, Kyosuke Nishida, Kuniko Saito

【用語解説】
※１．位置符号化　
LLM内部で単語の位置を表現する機構の総称です。位置埋め込みとも呼ばれます。LLMに入力された各単語の位置を、正弦波や余弦波または学習可能埋め込みなどを使って表現することが一般的です。

※２．Rotary Position Embedding (RoPE)　
回転行列を使った位置符号化手法です。絶対位置を採用しているため、高速かつ最大系列長内であれば性能が良いことから多くのLLMで採用されています。 LLM内部のクエリベクトルと回転行列を適用することで位置を表現します。キーベクトルに対しても同じ処理を行います。


※３．ウェーブレット変換　
信号処理において、信号を解析する時間周波数解析手法において代表的な手法です。ウェーブレットとは、ある区間にのみ波が存在する波形の総称です。信号を複数のウェーブレットに変換することで信号が持つ特徴を解析します。スケールとシフトという二つのパラメータを変えることで様々な分解能で信号が持つ特徴を抽出します。スケールはウェーブレットにおいて波が局在する範囲を指定でき、シフトは波が局在する場所をずらすことができます。同じく信号を解析する周波数解析であるフ―リエ変換はコサイン関数またはサイン関数に信号を変換することで信号が持つ特徴を解析します。フーリエ変換は時間的な特徴を捉えることができませんが、ウェーブレット変換は時間的な情報を捉えることが可能です。

※４．クエリベクトル、キーベクトル
LLM内部において、各単語は単語埋め込みベクトルと呼ばれるd個の数値に変換されます。このとき、dはモデルによって変わり、4000以上の数値で表現される場合もあれば、500程度の数値で表現される場合もあります。これらの数値をさらに、クエリベクトル、キーベクトル、バリューベクトルに３分割します。このとき、クエリベクトルは検索したい単語、キーベクトルとバリューベクトルは辞書として捉えることができます。

※５．注意スコア
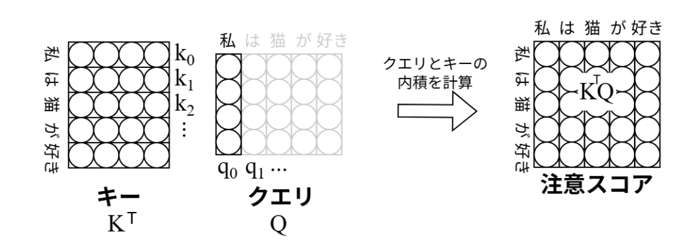
クエリベクトルとキーベクトルの内積を計算することで各単語が他の単語とどの程度関係しているかを計算します。このとき計算した値を注意スコアを呼びます。さらにそのあと注意スコアとバリューベクトルの内積を計算することでどの単語に着目すべきかを計算します。


図８：クエリベクトルとキーベクトルの内積を計算する。このとき計算した値が注意スコアと呼ばれる。

※６．Attention with Linear Bias (ALiBi)　
相対位置を考慮した線形バイアスを注意スコアに足し合わせることで位置を表現する位置符号化手法です。相対位置を採用しているため、最大系列長より長い文でも生成可能ですが、遠い依存関係にある単語の情報を取得できない、さらに最大系列長より短い文ではRoPEより性能が低いという課題もあります。


※7：Relative Position Representation (RPE)
クエリベクトルと、相対位置を表現した学習可能なパラメータの内積を計算することで位置を表現する位置符号化手法です。相対位置を採用していますが、ある一定の範囲内の相対位置しか表現しない（例えば、前後１６単語のみの相対位置を表現するなど。）ため、外挿性能や長文には不向きであると考えられます。


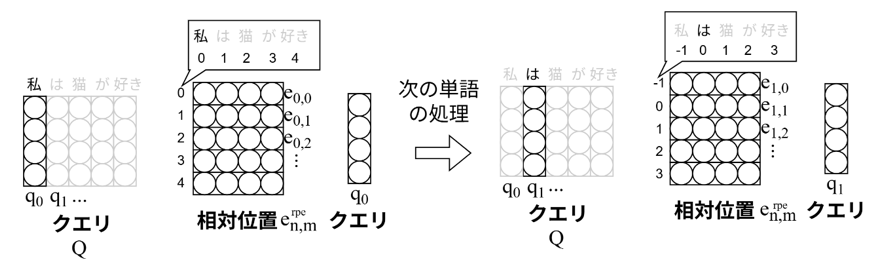
図１０：学習可能なパラメータで相対的な位置を表現し、クエリと内積を取ることで位置を表現するRelative Position Representation (RPE)の概要図。RPEでは相対位置は学習可能パラメータで表現される。本成果である「ウェーブレット位置符号化」はこの相対位置を学習可能パラメータではなく、ウェーブレット関数に基づいて計算します。